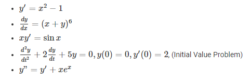Examples of differential equations with solutions

“Ordinary Differential Equations:-

           In mathematics, the term “Ordinary Differential Equations” also known as ODE is a relation that contains only one independent variable and one or more of its derivatives with respect to the variable. In other words, the ODE’S is represented as the relation having one real variable x, the real dependent variable y, with some of its derivatives.

Y’,y”, ….yn ,…with respect to x.

           The order of ordinary differential equations is defined to be the order of the highest derivative that occurs in the equation. The general form of n-th order ODE is given as;

F(x, y,y’,….,yn ) = 0

Note that, y’ can be either dy/dx or dy/dt and yn can be either dny/dxn or dny/dtn.

An n-th order ordinary differential equations is linear if it can be written in the form;

a0(x)yn + a1(x)yn-1 +…..+ an(x)y = r(x)

          (The function aj(x), 0≤j≤n are called the coefficients of the linear equation. The equation is said to be homogeneous if r(x)=0.If r(x)≠0 , it is said to be a non- homogeneous equation. Also, learn the first order differential equation here.)

Ordinary Differential Equations Types

              The ordinary differential equation is further classified into three types. They are:

• Autonomous ODE
• Linear ODE
• Non-linear ODE

Autonomous Ordinary Differential Equations

A differential equation which does not depend on the variable, say x is known as an autonomous differential equation.

Linear Ordinary Differential Equations

       If differential equations can be written as the linear combinations of the derivatives of y, then it is known as linear ordinary differential equations. It is further classified into two types,

• Homogeneous linear differential equations
• Non-homogeneous linear differential equations

Non-linear Ordinary Differential Equations

If differential equations cannot be written in the form of linear combinations of the derivatives of y, then it is known as non-linear ordinary differential equations.

Ordinary Differential Equations Application

ODEs has remarkable applications and it has the ability to predict the world around us. It is used in a variety of disciplines like biology, economics, physics, chemistry and engineering. It helps to predict the exponential growth and decay, population and species growth. Some of the uses of ODEs are:

• Modelling the growth of diseases
• Describes the movement of electricity
• Describes the motion of the pendulum, waves
• Used in Newton’s second law of motion and Law of cooling.

Ordinary Differential Equations Examples

Some of the examples of ODEs are as follows;

Ordinary Differential Equations Problems and Solutions

          The ordinary differential equations solutions are found in an easy way with the help of integration. Go through once and get the knowledge of how to solve the problem.   

👇👇👇👇👇👇👇👇👇👇👇👇👇👇

Question 1:

Find the solution to the ordinary differential equation y’=2x+1

Solution:

Given, y’=2x+1

Now integrate on both sides, ∫ y’dx = ∫ (2x+1)dx

Which gives, y=2x2/2+x+c

y=x2+x+c

Where c is an arbitrary constant.

Question 2:

Solve y4y’+ y’+ x2 + 1 = 0

Solution:

Take, y’ as common,

y'(y4+1)=-x2-1

Now integrate on both sides, we get

y55+y=−x33−x+c

Where c is an arbitrary constant.

     For more maths concepts, keep visiting BYJU’S and get various maths related videos to understand the concept in an easy and engaging way.

Imp.Q.

        Solve                Given that  is a solution.

sol.

     The given equation can be written in the standard form as 

                              ........(1)

Here 1+P+Q=0, therefore   is a part of the C.F. of the solution of equation (1).

putting    & the corresponding values of  in equation (1), we get

     or                         where        

  or              (on integration)

   or     

   The complete salution of equation (1) is              👈  Ans

Read More

Fourier Transform Question || Engineering mathematics

FOURIER TRANSFORM:-

The Fourier transform (FT)

        decomposes a function of time (a signal) into its constituent frequencies. This is similar to the way a musical chord can be expressed in terms of the volumes and frequencies of its constituent notes. The term Fourier transform refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of time. 


       The Fourier transform of a function of time is itself a complex-valued function of frequency, whose magnitude (modulus) represents the amount of that frequency present in the original function, and whose argument is the phase offset of the basic sinusoid in that frequency. The Fourier transform is not limited to functions of time, but the domain of the original function is commonly referred to as the time domain. There is also an inverse Fourier transform that mathematically synthesizes the original function from its frequency domain representation.



                        Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statistics as well as in the study of physical phenomena exhibiting normal distribution (e.g., diffusion). The Fourier transform of a Gaussian function is another Gaussian function. Joseph Fourier introduced the transform in his study of heat transfer, where Gaussian functions appear as solutions of the heat equation.                               

Definition

The Fourier transform of a function f is traditionally denoted ${\displaystyle {\hat {f}}}$, by adding a circumflex to the symbol of the function. There are several common conventions for defining the Fourier transform of an integrable function ${\displaystyle f:\mathbb {R} \to \mathbb {C} }$.^[1][2] One of them is

${\displaystyle {\hat {f}}(\xi )=\int _{-\infty }^{\infty }f(x)\ e^{-2\pi ix\xi }\,dx,}$

(Eq.1)

for any real number ξ.

                    A reason for the negative sign in the exponent is that it is common in electrical engineering to represent by ${\displaystyle f(x)=e^{2\pi i\xi _{0}x}}$ a signal with zero initial phase and frequency ${\displaystyle \xi _{0}.}$^{[3][remark 5]} The negative sign convention causes the product ${\displaystyle e^{2\pi i\xi _{0}x}e^{-2\pi i\xi x}}$ to be 1 (frequency zero) when ${\displaystyle \xi =\xi _{0},}$ causing the integral to diverge. The result is a Dirac delta function at ${\displaystyle \xi =\xi _{0}}$, which is the only frequency component of the sinusoidal signal ${\displaystyle e^{2\pi i\xi _{0}x}.}$

When the independent variable x represents time, the transform variable ξ represents frequency (e.g. if time is measured in seconds, then frequency is in hertz). Under suitable conditions, f is determined by ${\displaystyle {\hat {f}}}$ via the inverse transform:

${\displaystyle f(x)=\int _{-\infty }^{\infty }{\hat {f}}(\xi )\ e^{2\pi ix\xi }\,d\xi ,}$

(Eq.2)

for any real number x.

             The statement that f can be reconstructed from ${\displaystyle {\hat {f}}}$ is known as the Fourier inversion theorem, and was first introduced in Fourier's Analytical Theory of Heat, although what would be considered a proof by modern standards was not given until much later.The functions f and ${\displaystyle {\hat {f}}}$ often are referred to as a Fourier integral pair or Fourier transform pair.

              For other common conventions and notations, including using the angular frequency ω instead of the frequency ξ, see Other conventions and Other notations below. The Fourier transform on Euclidean space is treated separately, in which the variable x often represents position and ξ momentum. The conventions chosen in this article are those of harmonic analysis, and are characterized as the unique conventions such that the Fourier transform is both unitary on L² and an algebra homomorphism from L¹ to L^∞, without renormalizing the Lebesgue measure.

Many other characterizations of the Fourier transform exist. For example, one uses the Stone–von Neumann theorem: the Fourier transform is the unique unitary intertwiner for the symplectic and Euclidean Schrödinger representations of the Heisenberg group.

One Questions only important solution:-

 Q. Find the fourier transform of  pdf 

Read More

Fourier Transform

The Fourier Transform 


1.1 Fourier transforms as integrals 
      There are several ways to define the Fourier transform of a function f : R → C. In this section, we define it using an integral representation and state some basic uniqueness and inversion properties, without proof. Thereafter, we will consider the transform as being defined as a suitable limit of Fourier series, and will prove the results stated here.

 The Fourier Transform is one of deepest insights ever made. Unfortunately, the meaning is buried within dense equations:

Yikes. Rather than jumping into the symbols, let's experience the key idea firsthand. Here's a plain-English metaphor:

• What does the Fourier Transform do? _Given a smoothie, it finds the recipe.
• How? _Run the smoothie through filters to extract each ingredient.
• Why? _Recipes are easier to analyze, compare, and modify than the smoothie itself.
• How do we get the smoothie back? _Blend the ingredients.

Here's the "math English" version of the above:The Fourier Transform takes a time-based pattern, measures every possible cycle, and returns the overall "cycle recipe" (the amplitude, offset, & rotation speed for every cycle that was found).

Time for the equations? No! _Let's get our hands dirty and experience how any pattern can be built with cycles, with live simulations.

If all goes well, we'll have an aha!_moment and intuitively realize why the Fourier Transform is possible. We'll save the detailed math analysis for the follow-up.

This isn't a force-march through the equations, it's the casual stroll I wish I had. Onward!

function
Fourier transform--1	1
Fourier transform--cosine
Fourier transform--delta function
Fourier transform--exponential function
Fourier transform--Gaussian
Fourier transform--Heaviside step function
Fourier transform--inverse function
Fourier transform--Lorentzian function
Fourier transform--ramp function
Fourier transform--sine

Fourier transform formula PDF 

Read More