The Fourier Transform
1.1 Fourier transforms as integrals
There are several ways to define the Fourier transform of a function f : R → C. In this section, we define it using an integral representation and state some basic uniqueness and inversion properties, without proof. Thereafter, we will consider the transform as being defined as a suitable limit of Fourier series, and will prove the results stated here.
The Fourier Transform is one of deepest insights ever made. Unfortunately, the meaning is buried within dense equations:
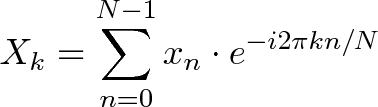
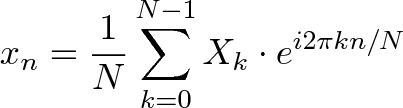
1.1 Fourier transforms as integrals
There are several ways to define the Fourier transform of a function f : R → C. In this section, we define it using an integral representation and state some basic uniqueness and inversion properties, without proof. Thereafter, we will consider the transform as being defined as a suitable limit of Fourier series, and will prove the results stated here.
The Fourier Transform is one of deepest insights ever made. Unfortunately, the meaning is buried within dense equations:
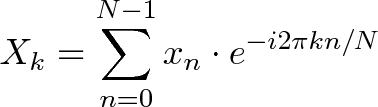
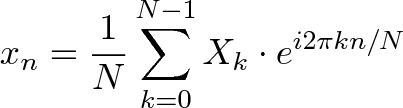
Yikes. Rather than jumping into the symbols, let's experience the key idea firsthand. Here's a plain-English metaphor:
- What does the Fourier Transform do? _Given a smoothie, it finds the recipe.
- How? _Run the smoothie through filters to extract each ingredient.
- Why? _Recipes are easier to analyze, compare, and modify than the smoothie itself.
- How do we get the smoothie back? _Blend the ingredients.
Here's the "math English" version of the above:The Fourier Transform takes a time-based pattern, measures every possible cycle, and returns the overall "cycle recipe" (the amplitude, offset, & rotation speed for every cycle that was found).
Time for the equations? No! _Let's get our hands dirty and experience how any pattern can be built with cycles, with live simulations.
If all goes well, we'll have an aha!_moment and intuitively realize why the Fourier Transform is possible. We'll save the detailed math analysis for the follow-up.
This isn't a force-march through the equations, it's the casual stroll I wish I had. Onward!
| function | ||
| Fourier transform--1 | 1 | |
| Fourier transform--cosine | ||
| Fourier transform--delta function | ||
| Fourier transform--exponential function | ||
| Fourier transform--Gaussian | ||
| Fourier transform--Heaviside step function | ||
| Fourier transform--inverse function | ||
| Fourier transform--Lorentzian function | ||
| Fourier transform--ramp function | ||
| Fourier transform--sine |














0 comments:
Post a Comment