Define Temperature Stresses :-
When ever there is some increase or decrease in temperature of a body, it cause the body to expand or contract. If the boys is allowed to expand or contract freely, with the rise or fall of the temperature, no stresses will be induced in the body. But if the deformation of the body is prevented some stresses are induced in the body. Such stresses are called thermal or temperature stresses.
The corresponding strains are called thermal & temperature strain.
Temperature stresses in beams or rods can be calculated as follows -
(i) Determine its expansion or contraction due to change in temperature assuming it is free to expand or contract.
(ii) Calculate the load required to bring the beam in original position.
(iii) Calculate stress and strain corresponding to this load.
l = Original length of the beam
t1 = Initial temperature of the beam
t2 = Final temperature of the beam
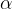 = Coefficient of linear expansion of beam material.
= Coefficient of linear expansion of beam material.
(Elongation of the beam due to increase in temperature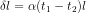
If elongation of the beam is prevented by some external force or by fixing its end, temperature strain will produced in beam, which is given by,
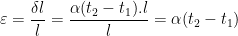
and temperature stress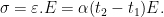
Q. A bar shown in fig. is subjected to axial forces and fixed at L and P. determine the forces in each portion of the bar and displacements of point M and N. Take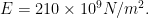
n
Sol =>
Given,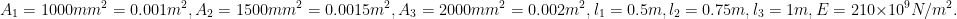
Forces in each portion
As we can see from figure, portion LM will be in tension, while portion NP will be in compression.
The free body diagram of all three portion are shown in fig.
Now, for static equilibrium of the bar,
R1+R2=100+50=150kN ........(1)
As bar is fixed at the ends, therefor extension of portion of portion LM will be equal to the compressions of MN & NP i.e,.
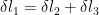
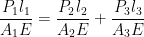
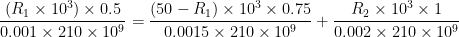
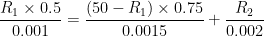
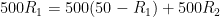
 ............(2)
............(2)
On solving equations (1)&(2), we get
 &
& 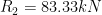
Hence, forces in each portion,
 66.67 kN (tensile)
66.67 kN (tensile)
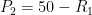
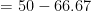
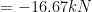
 16.67 kN (compressive) Ans
16.67 kN (compressive) Ans
& 83.33 kN (compressive ) Ans
83.33 kN (compressive ) Ans
Displacement of point M,
 0.1587 mm Ans
0.1587 mm Ans
Displacement of point N,
here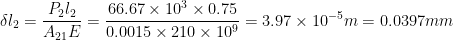
 Displacement of point N,
Displacement of point N,
 0.1984 mm Ans
0.1984 mm Ans
When ever there is some increase or decrease in temperature of a body, it cause the body to expand or contract. If the boys is allowed to expand or contract freely, with the rise or fall of the temperature, no stresses will be induced in the body. But if the deformation of the body is prevented some stresses are induced in the body. Such stresses are called thermal or temperature stresses.
The corresponding strains are called thermal & temperature strain.
Temperature stresses in beams or rods can be calculated as follows -
(i) Determine its expansion or contraction due to change in temperature assuming it is free to expand or contract.
(ii) Calculate the load required to bring the beam in original position.
(iii) Calculate stress and strain corresponding to this load.
l = Original length of the beam
t1 = Initial temperature of the beam
t2 = Final temperature of the beam
(Elongation of the beam due to increase in temperature
If elongation of the beam is prevented by some external force or by fixing its end, temperature strain will produced in beam, which is given by,
and temperature stress
Q. A bar shown in fig. is subjected to axial forces and fixed at L and P. determine the forces in each portion of the bar and displacements of point M and N. Take
n
Sol =>
Given,
Forces in each portion
As we can see from figure, portion LM will be in tension, while portion NP will be in compression.
The free body diagram of all three portion are shown in fig.
Now, for static equilibrium of the bar,
R1+R2=100+50=150kN ........(1)
As bar is fixed at the ends, therefor extension of portion of portion LM will be equal to the compressions of MN & NP i.e,.
On solving equations (1)&(2), we get
Hence, forces in each portion,
&
Displacement of point M,
Displacement of point N,
here
















0 comments:
Post a Comment