Stress and strain. Hook's Law

DEFINE STRESS AND STRAIN:-

Stress-
             When some external forces are applied to a body, it offers resistance to these forces. The magnitude of this resisting force is numerically equal to the applied forces. This internal resisting force per unit area is called stress. Therefore, stress can be defined as the intensity of internal forces resisting change in the shape of the body. It is calculated by simply dividing on an area divided by the a: ea. It is measured in N/m2 o: kg the force acting cm2. There are three types of stresses namely, tension, compression and shear. Mathematically,
                                                               Stress, a = P/A
                                   where,             P= Force applied
                                                          A=Cross-sectional area.
[जब कुछ बाहरी बलों को एक निकाय पर लागू किया जाता है, तो यह इन बलों के लिए प्रतिरोध प्रदान करता है। इस प्रतिरोध बल का परिमाण संख्यात्मक रूप से लागू बलों के बराबर होता है। प्रति इकाई क्षेत्र के इस आंतरिक प्रतिरोध बल को तनाव कहा जाता है। इसलिए, तनाव को शरीर के आकार में परिवर्तन का विरोध करने वाली आंतरिक शक्तियों की तीव्रता के रूप में परिभाषित किया जा सकता है। इसकी गणना केवल a: ea द्वारा विभाजित क्षेत्र पर विभाजित करके की जाती है। यह एन / एम 2 ओ में मापा जाता है: बल एक्टिंग सेमी 2 किग्रा। तनाव, संपीड़न और कतरनी जैसे तीन प्रकार के तनाव हैं.]


Types of Stresses;-
                                 The various types of stresses may be classified as follows-

(1) Simple or direct stress 
(a) Tension               (b) Compression         (3) shear

(2) Indirect stress
(a) Bending              (2) Torsion

(3) Combined stress



Strain-
              Strain is defined as the deformation or change produced in the dimensions of a body due to the effect of stress on it. It is a ratio of the change in dimension to the original dimension. Mathematically
                                   
                               
                                             Strain,                                                                                                                                         

                where, 


 

  


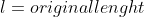
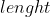
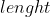
          Strain is a dimensionless quantity. Depending upon the type of stress, it where, can be of three types, namely tensile, compressive and shearing strain.



Types of Strain ;-
                           The various types of strains may be classified as follows-

(1) Tensile strain
(2) Compressive strain
(3) Shear strain
(4) Volumetric strain.


Hook's Law;-

Define:

                      According to Hook's law, when a material is loaded within its elastic limit, the stress is proportional to strain, or in other words, within elastic limits the ratio of stress in a material to the strain produced remains. Mathematical


                                                           

                                                                     


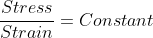
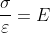
                 Where,
                               E is a constant of proportionality, which is called as a modulus of elasticity, or young's modulus. It has unit as the stress, i. e. or






Poisson's ratio;-
                                       Whenever body is stressed within elastic limits, it is subjected to both longitudinal and lateral deformation. The ratio of the lateral strain to longitudinal strain is a constant quantity for a material and this ratio is known as Poisson's ratio. This ratio is designated by 1/m or u. Mathematically,

Poisson's ratio, 1/m or





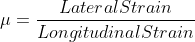
Thus,  
           

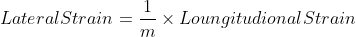
The limitation of Poisson's ratio is that it can be applied only when material is stressed within the elastic limits