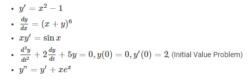Examples of differential equations with solutions

“Ordinary Differential Equations:-

           In mathematics, the term “Ordinary Differential Equations” also known as ODE is a relation that contains only one independent variable and one or more of its derivatives with respect to the variable. In other words, the ODE’S is represented as the relation having one real variable x, the real dependent variable y, with some of its derivatives.

Y’,y”, ….yn ,…with respect to x.

           The order of ordinary differential equations is defined to be the order of the highest derivative that occurs in the equation. The general form of n-th order ODE is given as;

F(x, y,y’,….,yn ) = 0

Note that, y’ can be either dy/dx or dy/dt and yn can be either dny/dxn or dny/dtn.

An n-th order ordinary differential equations is linear if it can be written in the form;

a0(x)yn + a1(x)yn-1 +…..+ an(x)y = r(x)

          (The function aj(x), 0≤j≤n are called the coefficients of the linear equation. The equation is said to be homogeneous if r(x)=0.If r(x)≠0 , it is said to be a non- homogeneous equation. Also, learn the first order differential equation here.)

Ordinary Differential Equations Types

              The ordinary differential equation is further classified into three types. They are:

• Autonomous ODE
• Linear ODE
• Non-linear ODE

Autonomous Ordinary Differential Equations

A differential equation which does not depend on the variable, say x is known as an autonomous differential equation.

Linear Ordinary Differential Equations

       If differential equations can be written as the linear combinations of the derivatives of y, then it is known as linear ordinary differential equations. It is further classified into two types,

• Homogeneous linear differential equations
• Non-homogeneous linear differential equations

Non-linear Ordinary Differential Equations

If differential equations cannot be written in the form of linear combinations of the derivatives of y, then it is known as non-linear ordinary differential equations.

Ordinary Differential Equations Application

ODEs has remarkable applications and it has the ability to predict the world around us. It is used in a variety of disciplines like biology, economics, physics, chemistry and engineering. It helps to predict the exponential growth and decay, population and species growth. Some of the uses of ODEs are:

• Modelling the growth of diseases
• Describes the movement of electricity
• Describes the motion of the pendulum, waves
• Used in Newton’s second law of motion and Law of cooling.

Ordinary Differential Equations Examples

Some of the examples of ODEs are as follows;

Ordinary Differential Equations Problems and Solutions

          The ordinary differential equations solutions are found in an easy way with the help of integration. Go through once and get the knowledge of how to solve the problem.   

👇👇👇👇👇👇👇👇👇👇👇👇👇👇

Question 1:

Find the solution to the ordinary differential equation y’=2x+1

Solution:

Given, y’=2x+1

Now integrate on both sides, ∫ y’dx = ∫ (2x+1)dx

Which gives, y=2x2/2+x+c

y=x2+x+c

Where c is an arbitrary constant.

Question 2:

Solve y4y’+ y’+ x2 + 1 = 0

Solution:

Take, y’ as common,

y'(y4+1)=-x2-1

Now integrate on both sides, we get

y55+y=−x33−x+c

Where c is an arbitrary constant.

     For more maths concepts, keep visiting BYJU’S and get various maths related videos to understand the concept in an easy and engaging way.

Imp.Q.

        Solve                Given that  is a solution.

sol.

     The given equation can be written in the standard form as 

                              ........(1)

Here 1+P+Q=0, therefore   is a part of the C.F. of the solution of equation (1).

putting    & the corresponding values of  in equation (1), we get

     or                         where        

  or              (on integration)

   or     

   The complete salution of equation (1) is              👈  Ans

Read More

Thermal stresses induced in bars of tapering section due to change in temperature_

Define Temperature Stresses :-


                 When ever there is some increase or decrease in temperature of a body, it cause the body to expand or contract. If the boys is allowed to expand or contract freely, with the rise or fall of the temperature, no stresses will be induced in the body. But if the deformation of the body is prevented some stresses are induced in the body. Such stresses are called thermal or temperature stresses.
                 The corresponding strains are called thermal & temperature strain.

                 Temperature stresses in beams or rods can be calculated as follows -
(i) Determine its expansion or contraction due to change in temperature assuming it is free to expand or contract.
(ii) Calculate the load required to bring the beam in original position.
(iii) Calculate stress and strain corresponding to this load.

 l = Original length of the beam
t1 = Initial temperature of the beam
t2 = Final temperature of the beam
 = Coefficient of linear expansion of beam material.
          (Elongation of the beam due to increase in temperature 
 If elongation of the beam is prevented by some external force or by fixing its end, temperature strain will produced in beam, which is given by,

                                

and temperature stress 




Q. A bar shown in fig. is subjected to axial forces and fixed at L and P. determine the forces in each portion of the bar and displacements of point M and N. Take  

         n
Sol     =>        

          Given,    




Forces in each portion 

   As we can see from figure, portion LM will be in tension, while portion NP will be in compression.
   The free body diagram of all three portion are shown in fig.
Now, for static equilibrium of the bar,

   
     R1+R2=100+50=150kN                       ........(1)
As bar is fixed at the ends, therefor extension of portion of portion LM will be equal to the compressions of MN & NP i.e,.
                                      

           

 

                 

                     

                   ............(2)

On solving equations (1)&(2), we get

 & 

Hence, forces in each portion,

      66.67 kN (tensile)                 

 

      

      

                 16.67 kN (compressive)              Ans

& 83.33 kN (compressive )              Ans

Displacement of point M,

 0.1587 mm    Ans

Displacement of point N,

here      

    Displacement of point N,

     0.1984 mm                    Ans

Read More

Fourier Transform Question || Engineering mathematics

FOURIER TRANSFORM:-

The Fourier transform (FT)

        decomposes a function of time (a signal) into its constituent frequencies. This is similar to the way a musical chord can be expressed in terms of the volumes and frequencies of its constituent notes. The term Fourier transform refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of time. 


       The Fourier transform of a function of time is itself a complex-valued function of frequency, whose magnitude (modulus) represents the amount of that frequency present in the original function, and whose argument is the phase offset of the basic sinusoid in that frequency. The Fourier transform is not limited to functions of time, but the domain of the original function is commonly referred to as the time domain. There is also an inverse Fourier transform that mathematically synthesizes the original function from its frequency domain representation.



                        Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statistics as well as in the study of physical phenomena exhibiting normal distribution (e.g., diffusion). The Fourier transform of a Gaussian function is another Gaussian function. Joseph Fourier introduced the transform in his study of heat transfer, where Gaussian functions appear as solutions of the heat equation.                               

Definition

The Fourier transform of a function f is traditionally denoted ${\displaystyle {\hat {f}}}$, by adding a circumflex to the symbol of the function. There are several common conventions for defining the Fourier transform of an integrable function ${\displaystyle f:\mathbb {R} \to \mathbb {C} }$.^[1][2] One of them is

${\displaystyle {\hat {f}}(\xi )=\int _{-\infty }^{\infty }f(x)\ e^{-2\pi ix\xi }\,dx,}$

(Eq.1)

for any real number ξ.

                    A reason for the negative sign in the exponent is that it is common in electrical engineering to represent by ${\displaystyle f(x)=e^{2\pi i\xi _{0}x}}$ a signal with zero initial phase and frequency ${\displaystyle \xi _{0}.}$^{[3][remark 5]} The negative sign convention causes the product ${\displaystyle e^{2\pi i\xi _{0}x}e^{-2\pi i\xi x}}$ to be 1 (frequency zero) when ${\displaystyle \xi =\xi _{0},}$ causing the integral to diverge. The result is a Dirac delta function at ${\displaystyle \xi =\xi _{0}}$, which is the only frequency component of the sinusoidal signal ${\displaystyle e^{2\pi i\xi _{0}x}.}$

When the independent variable x represents time, the transform variable ξ represents frequency (e.g. if time is measured in seconds, then frequency is in hertz). Under suitable conditions, f is determined by ${\displaystyle {\hat {f}}}$ via the inverse transform:

${\displaystyle f(x)=\int _{-\infty }^{\infty }{\hat {f}}(\xi )\ e^{2\pi ix\xi }\,d\xi ,}$

(Eq.2)

for any real number x.

             The statement that f can be reconstructed from ${\displaystyle {\hat {f}}}$ is known as the Fourier inversion theorem, and was first introduced in Fourier's Analytical Theory of Heat, although what would be considered a proof by modern standards was not given until much later.The functions f and ${\displaystyle {\hat {f}}}$ often are referred to as a Fourier integral pair or Fourier transform pair.

              For other common conventions and notations, including using the angular frequency ω instead of the frequency ξ, see Other conventions and Other notations below. The Fourier transform on Euclidean space is treated separately, in which the variable x often represents position and ξ momentum. The conventions chosen in this article are those of harmonic analysis, and are characterized as the unique conventions such that the Fourier transform is both unitary on L² and an algebra homomorphism from L¹ to L^∞, without renormalizing the Lebesgue measure.

Many other characterizations of the Fourier transform exist. For example, one uses the Stone–von Neumann theorem: the Fourier transform is the unique unitary intertwiner for the symplectic and Euclidean Schrödinger representations of the Heisenberg group.

One Questions only important solution:-

 Q. Find the fourier transform of  pdf 

Read More