De broglie wavelength equation (De-Broglie equation )

De Broglie Wavelength Formula

        In some situations, light behaves like a wave, while in others, it behaves like particles. The particles of light are called photons, and they can be thought of as both waves and particles. Louis de Broglie (1892-1987) developed a formula to relate this dual wave and particle behavior. It can also be applied to other particles, like electrons and protons. The formula relates the wavelength to the momentum of a wave/particle.

For particles with mass (electrons, protons, etc., but not photons), there is another form of the de Broglie wavelength formula. At non-relativistic speeds, the momentum of a particle is equal to its rest mass, m, multiplied by its velocity, v.

The unit of the de Broglie wavelength is meters (m), though it is often very small, and so expressed in nanometers (1 nm = 10(-9) m), or Angstroms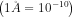  

 De broglie wavelength equation (De-Broglie equation )

     In 1924, Louis de-Broglie give the idea that matter should also posses dual nature. According to Louis de-Broglie a moving matter particle is surrounded by a wave whose wavelengths depend upon the mass of the particle and its velocity. These waves associated with the matter particles are known as matter waves or de-Broglie waves. The wavelength of the particle can be find through the following relation - 

                  

where h is the Planck's constant and p is the momentum of particle. The value of Planck's constant is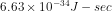 

 The de-Broglie concept of matter waves was based on the following facts- 

(i) Matter and light, both are forms of energy and each of them can be transformed into the other.

(ii) Both are governed by the space time symmetries of the theory of relativity.

Derive an expression for the de broglie wavelength:-

Considering the Planck's theory of radiation, the energy of the a photon (quantum) is given by

                              ......(1)

where c is the  velocity of light in vacuum and 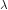 is its wavelength. 

According to Einstein energy mass relation 

                              ........(2)

From equation (1) & (2), we get 

             ........(3)

where mc = p (momentum associated with photon).

If we consider the case of a material particle of mass m and moving with a velocity v, then the wavelength associated with this particle is given by 

                       ..........(4)

If E is the kinetic energy of the material particle then 

                      

            .........(5)

Substituting the value of p in equation (4), we get  de broglie wavelength,

                ...........(6)

According to kinetic theory of gases, the average kinetic energy of particle is given by 

where, K=  Boltzmann's constant =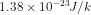 

Putting the value of E in equation (4)