Thermodynamic Scale of Temperature :- ABSOLUTE
An absolute temperature scale is independentof the properties of the substances.The temperatures are always measured by making use of properties e.g. thermal expansion of liquids and gases, the variation of thermo e.m.f. and electrical resistance with temperature etc.
Lord kelvin from the study of the effeciency of reversible engion could define a new scale of temperature which a independent of the particular substance because the efdficency of a reversible engion itself is independent of the working substance
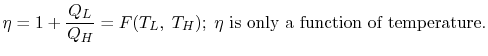 Also
Also
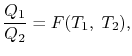
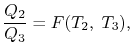
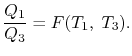 But
But
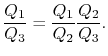 Hence
Hence
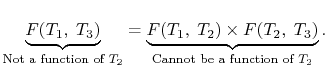
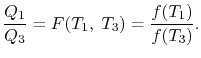 In general,
In general,
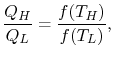
so that the ratio of the heat exchanged is a function of the temperature. We could choose any function that is monotonic, and one choice is the simplest: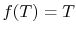 . This is the thermodynamic scale of temperature,
. This is the thermodynamic scale of temperature, 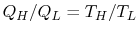 . The temperature defined in this manner is the same as that for the ideal gas; the thermodynamic temperature scale and the ideal gas scale are equivalent..
. The temperature defined in this manner is the same as that for the ideal gas; the thermodynamic temperature scale and the ideal gas scale are equivalent..

An absolute temperature scale is independentof the properties of the substances.The temperatures are always measured by making use of properties e.g. thermal expansion of liquids and gases, the variation of thermo e.m.f. and electrical resistance with temperature etc.
Lord kelvin from the study of the effeciency of reversible engion could define a new scale of temperature which a independent of the particular substance because the efdficency of a reversible engion itself is independent of the working substance
6.2 The Thermodynamic Temperature Scale;-
suryakanu.blogspot.com
Absolute temperature scale, any thermometric scale on which a reading of zero coincides with the theoretical absolute zero of temperature—i.e., the thermodynamic equilibrium state of minimum energy. The standard measure of temperature in the International System of Units is the Kelvin (K) scale, on which the only point established by arbitrary definition is the unique temperature at which the liquid, solid, and vapour forms of water can be maintained simultaneously. The interval between this temperature and absolute zero is defined as 273.16 kelvins, and the temperature of this “triple point” is designated 273.16 K (since 1967, no longer written °K). In essence, the Kelvin scale is the Celsius (°C) temperature scale shifted by 273.15 degrees (because the triple point of water is actually 0.01 °C), with the same size unit of temperature.
(The considerations of Carnot cycles in this section have not mentioned the working medium. They are thus not limited to an ideal gas and hold for Carnot cycles with any medium. )
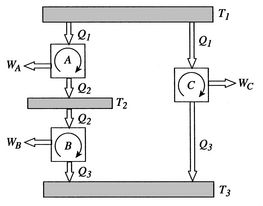
More specifically, we can define a thermodynamic temperature scale that is independent of the working medium. Earlier we derived the Carnot efficiency with an ideal gas as a medium and the temperature definition used in the ideal gas equation was not essential to the thermodynamic arguments. To see this, consider the situation shown below in Figure 6.2, which has three reversible cycles. There is a high temperature heat reservoir at 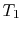 and a low temperature heat reservoir at
and a low temperature heat reservoir at 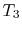 . For any two temperatures
. For any two temperatures 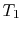 ,
, 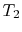 , the Ratio of the magnitudes of the heat absorbed and rejected in a Carnot cycle has the same value for all systems.
, the Ratio of the magnitudes of the heat absorbed and rejected in a Carnot cycle has the same value for all systems.
We choose the cycles so 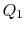 is the same for A and C. Also
is the same for A and C. Also 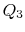 is the same for B and C. For a Carnot cycle
is the same for B and C. For a Carnot cycle
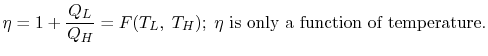
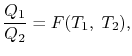
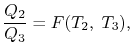
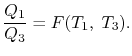
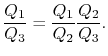
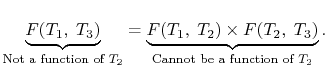
We thus conclude that 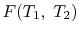 has the form
has the form 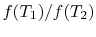 , and similarly
, and similarly 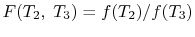 . The ratio of the heat exchanged is therefore
. The ratio of the heat exchanged is therefore
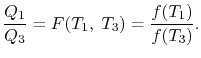
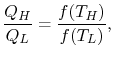
so that the ratio of the heat exchanged is a function of the temperature. We could choose any function that is monotonic, and one choice is the simplest:















0 comments:
Post a Comment