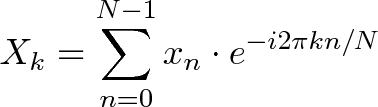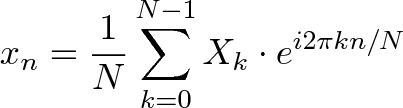Fourier Transform Question || Engineering mathematics

FOURIER TRANSFORM:-

The Fourier transform (FT)

        decomposes a function of time (a signal) into its constituent frequencies. This is similar to the way a musical chord can be expressed in terms of the volumes and frequencies of its constituent notes. The term Fourier transform refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of time. 


       The Fourier transform of a function of time is itself a complex-valued function of frequency, whose magnitude (modulus) represents the amount of that frequency present in the original function, and whose argument is the phase offset of the basic sinusoid in that frequency. The Fourier transform is not limited to functions of time, but the domain of the original function is commonly referred to as the time domain. There is also an inverse Fourier transform that mathematically synthesizes the original function from its frequency domain representation.



                        Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statistics as well as in the study of physical phenomena exhibiting normal distribution (e.g., diffusion). The Fourier transform of a Gaussian function is another Gaussian function. Joseph Fourier introduced the transform in his study of heat transfer, where Gaussian functions appear as solutions of the heat equation.                               

Definition

The Fourier transform of a function f is traditionally denoted ${\displaystyle {\hat {f}}}$, by adding a circumflex to the symbol of the function. There are several common conventions for defining the Fourier transform of an integrable function ${\displaystyle f:\mathbb {R} \to \mathbb {C} }$.^[1][2] One of them is

${\displaystyle {\hat {f}}(\xi )=\int _{-\infty }^{\infty }f(x)\ e^{-2\pi ix\xi }\,dx,}$

(Eq.1)

for any real number ξ.

                    A reason for the negative sign in the exponent is that it is common in electrical engineering to represent by ${\displaystyle f(x)=e^{2\pi i\xi _{0}x}}$ a signal with zero initial phase and frequency ${\displaystyle \xi _{0}.}$^{[3][remark 5]} The negative sign convention causes the product ${\displaystyle e^{2\pi i\xi _{0}x}e^{-2\pi i\xi x}}$ to be 1 (frequency zero) when ${\displaystyle \xi =\xi _{0},}$ causing the integral to diverge. The result is a Dirac delta function at ${\displaystyle \xi =\xi _{0}}$, which is the only frequency component of the sinusoidal signal ${\displaystyle e^{2\pi i\xi _{0}x}.}$

When the independent variable x represents time, the transform variable ξ represents frequency (e.g. if time is measured in seconds, then frequency is in hertz). Under suitable conditions, f is determined by ${\displaystyle {\hat {f}}}$ via the inverse transform:

${\displaystyle f(x)=\int _{-\infty }^{\infty }{\hat {f}}(\xi )\ e^{2\pi ix\xi }\,d\xi ,}$

(Eq.2)

for any real number x.

             The statement that f can be reconstructed from ${\displaystyle {\hat {f}}}$ is known as the Fourier inversion theorem, and was first introduced in Fourier's Analytical Theory of Heat, although what would be considered a proof by modern standards was not given until much later.The functions f and ${\displaystyle {\hat {f}}}$ often are referred to as a Fourier integral pair or Fourier transform pair.

              For other common conventions and notations, including using the angular frequency ω instead of the frequency ξ, see Other conventions and Other notations below. The Fourier transform on Euclidean space is treated separately, in which the variable x often represents position and ξ momentum. The conventions chosen in this article are those of harmonic analysis, and are characterized as the unique conventions such that the Fourier transform is both unitary on L² and an algebra homomorphism from L¹ to L^∞, without renormalizing the Lebesgue measure.

Many other characterizations of the Fourier transform exist. For example, one uses the Stone–von Neumann theorem: the Fourier transform is the unique unitary intertwiner for the symplectic and Euclidean Schrödinger representations of the Heisenberg group.

One Questions only important solution:-

 Q. Find the fourier transform of  pdf 

Read More

Solidification of metals animation

Solidification of pure metals take place animation:-


                Solidification is the transformation of materials from the liquid the solid crystalline state on cooling.During solidification, the disordered structure of the liquid transforms to the orderly arrangement characteristic of the crystal. This process of solidification does not occur instantaneously. The process is characterized by the formation of numerous small particles of the new phase (s), which increase in size until the transformation completes. The process of solidification may be broken down into two stages-nucleation and grain growth. Nucleation involves the appearance of very small particles called nuclei, these nuclei then grow in size, untill the phase transformation is complete.

solidification of metals animation

            All solid metals are crystalline and crystals or grains are made up of several atoms. These individual crystals or grains are aggregated to form a visible mass of solid metal. These grains are formed when liquid metal solidifies. The process of solidification starts when liquid metal cooled below the equilibrium temperature (the temperature at which given metal exist simultaneously solid and liquid phase).
 Solidification starts when two or more atoms associate themselves to form very small crystal called nuclei. This may happen simultaneously at a Number of locations throughout the liquid metal. At these points a few atoms assume an orderly arrangement to give the unit cubic structure and growth takes place in three dimensional as shown in fig. As a result of this growth tree like crystals known as dendrites  [arise from Greek word dendrom  meaning tree ] are formed. A dendrite consists of unit cell, which are exceedingly small, first form in a straight line.




Slow rate of cooling promotes crystallization while a faster cooling rate of cooling rate may prevent crystallization. 

Read More

Types of SAND in civil Engineering

Types of sand according to size:-

GREEN SAND

DRY SAND

LOAM SAND

FACING SAND

BACKING SAND

SYSTEM SAND

PARTING SAND

CORE SAND


Define all types SAND:_-

          GREEN SAND- It is a mixture of silica sand with 18 to 30 percent clay, having a total water content 6 to 8 percent. The clay and water furnish the bond for green sand. It is fine, soft, light, and porous. Being damp when squeezed in the hand, it retains the shape, the impression given to it under pressure. Moulds prepared in this sand are known as green sand moulds.


           DRY SAND- Green sand that has been dried or baked after the mould is made is called dry sand. They are suitable for larger castings. Moulds prepared in this sand are known as dry sand.


            LOAM SAND- Loam Sand is high in clay, as much as 50 percent  or so, and dries hard. This is particularly employed for laom moulding usually for large castings.


            FACING SAND- Facing sand forms the face of the mould. It is used directly next to the surface of the pattern and it comes into contact with the molten metal when the mould is poured. Consequently, it is subjected to the the severest conditions and therefore, must possess, high strength and ls with refractoriness. It is made of silica sand and clay, without the addition of used sand. Different forms of carbon are uscd to prevent the metal from burning into the sand. They are sometimes mixed with 6 to 15 times as much fine moulding sand to make facings.


          BACKING SAND- Backing sand or floor sand or floor sand is used to back up the facing sand and to fill the whole volume of the flask. Old, repeatedly used moulding sand is mainly employed for this purpose.
     The backing sand is sometimes called black sand because of the fact that old, repeatedly used moulding sand is black in colour due to the addition of coal dust and burning on coming in contact with molten metal.


           SYSTEM SAND-In mechanical preparation and handling unit, no facing sand is used. The used sand is cleaned and reactivated by the addition binder in of water binders and special additives. This is known as system sand, In etimes mechanical foundries, where machine moulding is employed so called system sand is used to fill the whole flask. Since the whole mould is made of this system sand therefore, strength, permeability and refractoriness of this sand must be higher than those of backing sand.


              PARTING SAND-Parting sand is used to prevent the green sand from sticking to the pattern and also to allow the sand on the parting surface of the cope and drag to separate without clinging. This is clean clay-free silica sand which serves the same purpose as parting dust


              CORE SAND- Sand used for making cores is called core sand sometimes called oil sand. This is silica oil sand. This is silica sand mixed with core oil which is composed of linseed oil, resin, light mineral oil and other binding materials. Pitch or flours and water may be used in larger cores for the sake of economy.

Types of SAND in civil Engineering

Read More

Stress and strain. Hook's Law

DEFINE STRESS AND STRAIN:-

Stress-
             When some external forces are applied to a body, it offers resistance to these forces. The magnitude of this resisting force is numerically equal to the applied forces. This internal resisting force per unit area is called stress. Therefore, stress can be defined as the intensity of internal forces resisting change in the shape of the body. It is calculated by simply dividing on an area divided by the a: ea. It is measured in N/m2 o: kg the force acting cm2. There are three types of stresses namely, tension, compression and shear. Mathematically,
                                                               Stress, a = P/A
                                   where,             P= Force applied
                                                          A=Cross-sectional area.
[जब कुछ बाहरी बलों को एक निकाय पर लागू किया जाता है, तो यह इन बलों के लिए प्रतिरोध प्रदान करता है। इस प्रतिरोध बल का परिमाण संख्यात्मक रूप से लागू बलों के बराबर होता है। प्रति इकाई क्षेत्र के इस आंतरिक प्रतिरोध बल को तनाव कहा जाता है। इसलिए, तनाव को शरीर के आकार में परिवर्तन का विरोध करने वाली आंतरिक शक्तियों की तीव्रता के रूप में परिभाषित किया जा सकता है। इसकी गणना केवल a: ea द्वारा विभाजित क्षेत्र पर विभाजित करके की जाती है। यह एन / एम 2 ओ में मापा जाता है: बल एक्टिंग सेमी 2 किग्रा। तनाव, संपीड़न और कतरनी जैसे तीन प्रकार के तनाव हैं.]


Types of Stresses;-
                                 The various types of stresses may be classified as follows-

(1) Simple or direct stress 
(a) Tension               (b) Compression         (3) shear

(2) Indirect stress
(a) Bending              (2) Torsion

(3) Combined stress



Strain-
              Strain is defined as the deformation or change produced in the dimensions of a body due to the effect of stress on it. It is a ratio of the change in dimension to the original dimension. Mathematically
                                   
                               
                                             Strain,                                                                                                                                         

                where, 


 

  


          Strain is a dimensionless quantity. Depending upon the type of stress, it where, can be of three types, namely tensile, compressive and shearing strain.



Types of Strain ;-
                           The various types of strains may be classified as follows-

(1) Tensile strain
(2) Compressive strain
(3) Shear strain
(4) Volumetric strain.


Hook's Law;-

Define:

                      According to Hook's law, when a material is loaded within its elastic limit, the stress is proportional to strain, or in other words, within elastic limits the ratio of stress in a material to the strain produced remains. Mathematical


                                                           

                                                                     


                 Where,
                               E is a constant of proportionality, which is called as a modulus of elasticity, or young's modulus. It has unit as the stress, i. e. or






Poisson's ratio;-
                                       Whenever body is stressed within elastic limits, it is subjected to both longitudinal and lateral deformation. The ratio of the lateral strain to longitudinal strain is a constant quantity for a material and this ratio is known as Poisson's ratio. This ratio is designated by 1/m or u. Mathematically,

Poisson's ratio, 1/m or





Thus,  
           

The limitation of Poisson's ratio is that it can be applied only when material is stressed within the elastic limits

Read More

Casting process steps

CASTING PROCESS


Define ;-(casting)

          [ In casting, the molten metal is poured into a refractory mould with a cavity of the shape to be made, and allowed to solidify.After solidification, the desired metal object is taken out from the mould. The solidified object is known as casting. Sand moulds are generally used for casting, however, they cannot maintain better tolerances and smooth surface finish. Thus, now-a- 104days metallic moulds are more common.]

[कास्टिंग में, पिघली हुई धातु को एक आग रोक साँचे में डाला जाता है, जिसे आकार की एक गुहा के साथ बनाया जाता है, और जमने दिया जाता है। जमने के बाद, वांछित धातु की वस्तु को साँचे से बाहर निकाल लिया जाता है। जमना वस्तु कास्टिंग के रूप में जाना जाता है। आम तौर पर कास्टिंग के लिए सैंड मोल्ड का उपयोग किया जाता है, हालांकि, वे बेहतर सहनशीलता और चिकनी सतह खत्म नहीं कर सकते हैं। इस प्रकार, अब- a- 104days धातु के सांचे अधिक आम हैं।]

            Various casting processes are as follows- 

(i)        Sand casting 
(ii)       Plaster mould casting
(iii)      Vacuum casting
(iv)      Investment casting
(v)       Slush casting
(vi)      Pressure casting
(vii)     Centrifugal casting
(viii)    Continuous casting
(ix)      Squeeze casting
(x)       Shell mould casting
(xi)      Die casting


Applications of Casting-

(i) Automobile parts such as engine blocks, cylinder blocks, pistons, piston rings, etc
(ii) Machine tool structures, e.g. planar beds.
(iii) Wheels and housings of steam and hydraulic turbines, turbine vanes and aircraft jet engine blades.
(iv) Railway crossings (Mn-steel cast section)
(v) Supercharger casing
(vi) Water supply and sewer pipes
(vii) Sanitary fittings
(ix) Agriculture part
(x) Communication,

Define;-(Moulding)

      Moulding can be defined as a process of making sound mould of sand by using pattern and cores, so that the metal can be poured into the moulds to produce casting.


MOULDING & CASTING PROCESS_

         (I) Expendables mould casting -
                       In this type of casting processes, the mould cavity is obtained by consolidating a moulding material around a pattern. The commonly used moulding material for these processes is sand or some other refractory material. Because of the sand moulding the dimensions accuracy and surface finish of the casting are not up to the requirements of modern  Industries.

NATURAL SEE

(II) Permanent Mould Casting;- 
                    In type of casting processes, the mould is not destroyed after the solidification of the casting and can be used repeatedly. These moulds are adaptable to the production of tens and thousands of castings. The products of this process have smooth surface and better dimensional accuracy. Due to the high cost of permanent moulds their use is limited to mass production of small and medium sized parts of light non- ferrous alloys

(iii) Semi-permanent Mould Casting;-
                 In this type of casting processes, moulds are prepared from high refractory materials like graphite These moulds are less durable as compared to permanent moulds and can only be used for few tens of castings.

Properties of sand in construction

(1) Porosity
(2) Flowability
(3) Collapsibility
(4) Adhesiveness
(5) Cohesiveness or Strength
(6) Refractoriness
(7) Chemical Resistivity

casting process download pdf

Read More

Fourier Transform

The Fourier Transform 


1.1 Fourier transforms as integrals 
      There are several ways to define the Fourier transform of a function f : R → C. In this section, we define it using an integral representation and state some basic uniqueness and inversion properties, without proof. Thereafter, we will consider the transform as being defined as a suitable limit of Fourier series, and will prove the results stated here.

 The Fourier Transform is one of deepest insights ever made. Unfortunately, the meaning is buried within dense equations:

Yikes. Rather than jumping into the symbols, let's experience the key idea firsthand. Here's a plain-English metaphor:

• What does the Fourier Transform do? _Given a smoothie, it finds the recipe.
• How? _Run the smoothie through filters to extract each ingredient.
• Why? _Recipes are easier to analyze, compare, and modify than the smoothie itself.
• How do we get the smoothie back? _Blend the ingredients.

Here's the "math English" version of the above:The Fourier Transform takes a time-based pattern, measures every possible cycle, and returns the overall "cycle recipe" (the amplitude, offset, & rotation speed for every cycle that was found).

Time for the equations? No! _Let's get our hands dirty and experience how any pattern can be built with cycles, with live simulations.

If all goes well, we'll have an aha!_moment and intuitively realize why the Fourier Transform is possible. We'll save the detailed math analysis for the follow-up.

This isn't a force-march through the equations, it's the casual stroll I wish I had. Onward!

function
Fourier transform--1	1
Fourier transform--cosine
Fourier transform--delta function
Fourier transform--exponential function
Fourier transform--Gaussian
Fourier transform--Heaviside step function
Fourier transform--inverse function
Fourier transform--Lorentzian function
Fourier transform--ramp function
Fourier transform--sine

Fourier transform formula PDF 

Read More